Philosophical impact on selection rules and practical impacts of those for cooperative groups
All following considerations are in a zone of extreme consent, where no one is consciously forced into action or impacted against their will. This is tricky, because everything is quite heavily linked in the biosphere of Earth: those who choose to drive sports cars contribute more to the flooding of islands than those who drive small cars. But for now, excuse all those sports car drivers who do not realize the impact of their actions.
Let happiness imply some kind of desirable quality, e.g. pleasure and let suffering imply some kind of undesirable quality, e.g. pain. Happiness and suffering are experienced due to action.
When deciding on actions, let enthusiasm prospectively map onto happiness and resistance prospectively map onto suffering. Let _acceptance
Philosophy: Utility
"It is the greatest good to the greatest number of people which is the measure of right and wrong.
-- Jeremy Bentham, 1780
Happiness and suffering are of equal weight,
Choose the action with the greatest sum of happiness subtracting suffering,
Logic: Majority
Since happiness and suffering are of equal weight, simply consider what people support and count anything else as resistance. Select action with most support,
- Plurality. (a.k.a relative majority) Choose action with most support (> 1 %)
- Majority. (a.k.a. absolute majority) Choose action with over half supporting (> 50 %)
- Supermajority. (a.k.a. 'consensus') Choose action with significantly more than half supporting (often 66.6 %, 75 %, 80 % or 90%)
- Unanimous support. Choose the action total support (100 %)
Some things will be done that a significant number do not want, leading to minoritization.
Philosophy: Negative Utility (Absolute)
"there is ... no symmetry between suffering and happiness ... human suffering makes a direct moral appeal, namely, the appeal for help, while there is no similar call to increase the happiness of a man who is doing well anyway. ... the Utilitarian formula "Maximize pleasure" ... assumes a continuous pleasure-pain scale which allows us to treat degrees of pain as negative degrees of pleasure. ... Instead of the greatest happiness for the greatest number, one should demand, more modestly, the least amount of avoidable suffering for all..."
-- Karl Popper, 1940
Suffering is of infinitely greater weight than happiness,
Choose the action with the least sum of suffering,
Logic: Consensus
Since suffering is of infinitely greater weight than happiness, simply consider what people resist. Consider the inverse of resistance to be acceptance. Select action with least resistance/most acceptance,
- Unanimous acceptance Choose action with total acceptance (100 %)
- Unanimous acceptance - n Choose action with total acceptance subtracting some constanct (often '-1' or '-2' people, percentage differs with group size)
- Maximum acceptance Choose action with most acceptance (> 1 %)
Philosophy: Negative Leaning Utility
Suffering is of significantly more weight than happiness,
Choose the action with the greatest sum of happiness subtracting weighted suffering,
(Where is some factor increasing the weight of suffering)
Holomajoritarianism
Since suffering is of significantly greater weight than happiness but happiness is not negligible both must be considered, unequally. Select action with most acceptance and most support based on some weight ratio.
- See Utilitarianism ^
- See Negative Utilitarianism ^
- Choose action with with greatest acceptance, considering support.
Foreword
About a week ago I described our implementation of Systemic Consensus on a mailing list for election science, 'Our group uses Systemic Consensus: Negative Score Voting w. control options and consensus logic.' I promptly got a response from William Waugh:
"If the ranges of two score voting systems can be mapped to each other as y=mx+c, those systems are strategically equivalent. Your choice of putting the top of the scale at nominal zero may have a psychological effect on some voters, but it does not change the nature of the voting system itself viewed as a game."
This sent me on a bit of a vision quest where I have come to the somewhat unsettling conclusion that the 'most accepted' meme is a consensus trilemma: a group of cooperative individuals who refuse to be dominated must choose one of the following to increase the exclusivity of a group (and limit growth and diversity) to endure an increase in group member dishonesty (and decrease trust and cooperation) or to change the meme to 'most accepted but support not ignored' (and have a slight increase in minority domination).
Coordination games
Group decision making processes are games. Players are faced with a number options and a standard way to express their opinion on them. The player opinions are aggregated and an option is selected as a decision on the basis of some rule. The way of expression, the method of aggregation and the selection rule are constructed on the basis of some logic which is ultimately founded on some belief.
Why bother?
Although you can do what you want, you may be more successful at getting what you want by doing things with other people. It's also more fun. (See division of labor, economy of scale). Perhaps everyone intuitively thinks exactly the same... but what happens when there is dissent: disagreement, difference, etc? Decisions are a coordination concept which can be vague or contractual. Coordination makes collaboration easier and prevents unnecessary conflicts.
Faith on pleasure and suffering
Faith offers lot's of advice on what to do and not do.
2100 BC, Sumerian civilization: importance = pleasure
"Fill your belly. Day and night make merry. Let days be full of joy. Dance and make music day and night [...] These things alone are the concern of men" -- Old Babylonian version of the Epic of Gilgamesh, Siduri.
2000 BC, Judaism: sufferingquantityquality = sufferingquantityquality
24 Eye for eye, tooth for tooth, hand for hand, foot for foot, 25 Burning for burning, wound for wound, stripe for stripe. (Exo 21:24-25, a.k.a lex talionis)
500 BC, Buddhism: importance = no (existential) suffering
Now this, bhikkhus, is the noble truth of the way leading to the cessation of suffering: it is this noble eightfold path; that is, right view ... right concentration (Dhammacakkapavattana Sutta, Samyutta Nikaya LVI, 11, a.k.a. the Fourth Noble Truth)
30 AD, Christianity: pleasure for you = pleasure for others
31 And as ye would that men should do to you, do ye also to them likewise. (Luke 6:31)
30 AD, Christianity: suffering → not(suffering)/pleasure
38 Ye have heard that it hath been said, An eye for an eye, and a tooth for a tooth: 39 But I say unto you, That ye resist not evil: but whosoever shall smite thee on thy right cheek, turn to him the other also. (Matt 5:38-39)
Whilst offering a lot ideas for personal decision making, faith doesn't make help so much with complex cooperation, coordination or collaboration.
Utilitarian philosophy
Utilitarianism is about maximising total utility of multiple individuals. Utility is generically defined as the maximization of some desired measure and/or the minimization of some undesired measure.
1780: Jeremy Bentham: greatest good = ↑𝚺(pleasurequantity-painquantity) [pleasure = -suffering]
1860, John Stuart Mill: greatest good = ↑𝚺(pleasurequantityquality-painquantityquality) [pleasure = -suffering]
500 BC, Epicurus: greatest good = ↑𝚺(pleasure-pain) [pleasure = -suffering]
1940, Karl Popper: greatest good = ↓𝚺(painquantityquality) [not(suffering) >> pleasure]
"there is, from the ethical point of view, no symmetry between suffering and happiness, or between pain and pleasure… In my opinion human suffering makes a direct moral appeal, namely, the appeal for help, while there is no similar call to increase the happiness of a man who is doing well anyway. A further criticism of the Utilitarian formula "Maximize pleasure" is that it assumes a continuous pleasure-pain scale which allows us to treat degrees of pain as negative degrees of pleasure. But, from the moral point of view, pain cannot be outweighed by pleasure, and especially not one man's pain by another man's pleasure. Instead of the greatest happiness for the greatest number, one should demand, more modestly, the least amount of avoidable suffering for all..."
Some 20th century categorization
Cooperative and collaborative:
- Consent: Can you find an option you both support?
- Compromize: Can you both compromize to find the most mutually acceptable option?
Not cooperative, but still collaborative:
- Delegation: Can you both accept the judgement of a third party or some agent of chance?
- Domination: Can you persuade the other to compromize and accept your preference?
Neither cooperative nor collaborative:
- Flight: Parties avoid each other. (→ fragmentation of group)
- Destruction: Parties try and dominate the other and refuse to be dominated. (→ conflict and escalation thereof)
Theory on Social Choice
Social choice theory or social choice is a theoretical framework for analysis of combining individual opinions, preferences, interests, or welfares to reach a collective decision or social welfare in some sense. -- wikipedia
Instead of just guessing what people are thinking and acting on their behalf, it is possible to ask people for their opinions and act on that basis. This process of selecting an action can be called group decision making. Decisions can be seen more like coordination events or contracts. Given a set of expressions, how they are aggregated and how a selection is made from that aggregation is based upon a logic based upon a philosophy.
Any GDM process can be considered as a game: how that game is constructed, selected and played depends upon the players concept of utility. At scale, conversation becomes impractical due to physical and temporal restrictions and favors dominant behavior. Voting systems allow basically any number of people to express themselves with equal weight, although different systems permit different expressions.
Single vote systems only permit the expression of the most preferred option.
Ranked vote systems permit the indication of the order of preference (e.g. apples:1st, oranges:2nd, pears:3rd). This implies the concept of ordinal utility since you can say that apples are more preferable than oranges, but you cannot say whether apples are two time more preferable or twenty times.
Rated voting systems permit the expression of order of preference and magnitude (e.g. apples:10, oranges:2, pears:1). This implies the concept of cardinal utility since you can say that apples are more preferable than oranges and that they are 5 times more preferable. 'Utils' are arbitrary units of cardinal utility.
The increase in expressivity of systems can be seen considering the number of distinct expressions relate to the number of available options,
On the basis that for any meaningful number of levels rated vote systems provide the greatest degree of expressivity, that greater expressivity permits more honest expression and that more honesty leads to more trust and cooperation, only those systems are further considered. Cardinal utility is hence assumed to be valid.
After individuals have expressed themselves, these expressions must be aggregated and some selection rule applied. Aggregating ratings is a trivial case of multiplication and addition. A majoritarian (dominative) selection meme is that of 'most support', whereby that which is not support is resistance, If you're not for it, you're against it
On the ground
With a relatively small number of people it is often possible to find consent or compromise informally, conversationally and with everyone on the same level. (See Advice Process, Doocracy and NVC). With more people, you still can - but it becomes increasingly difficult: limitations in space and time can lead to domination by a minority of people with more meeting flexibility, louder voices or manipulative rhetoric.
Philosophy * Social Choice Theory
Majority is a fairly well known concept: What do most people want? Since what people want is related to what they don't want, we can say majority is a dominative, utilitarian approach, ↑𝚺(pleasure-pain). The majority approach is a dominative approach in which the most preferred option of a majority are selected. The good thing is that a minority of individuals cannot dominate a majority, the bad thing is that it's possible a significant number of people will be unhappy with an outcome - perhaps even more than half. In an environment without the use of force, this can lead to conflict and fragmentation. Single vote and ranked vote systems are a common implementations of this approach.
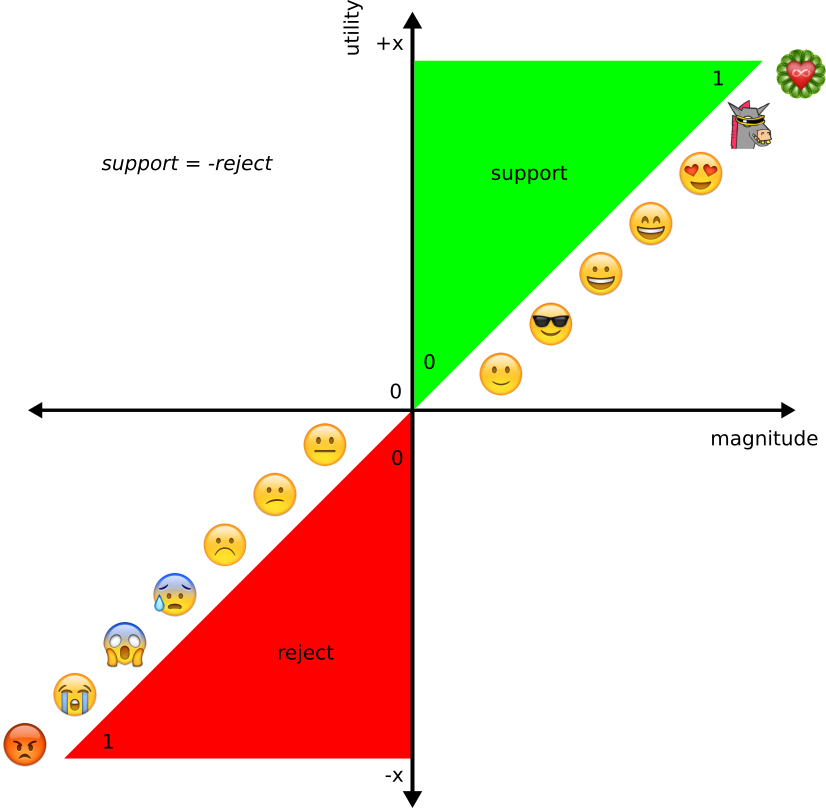
Consensus has at least three distinct concepts:
- The absence of rejection. Veto/block, activist groups, housing projects, religious groups, etc.
- Some vague support supermajority. Science, politics, medical, 'U-1/-2', etc
- That which is most acceptable. Systemisches Konsensieren Prinzip Using the final concept as the definition of consensus hereon, we can say majoirty is a cooperative, negative utilitarian approach, ↓𝚺(pain). It stands that support could be considered in the likelihood of tied options.
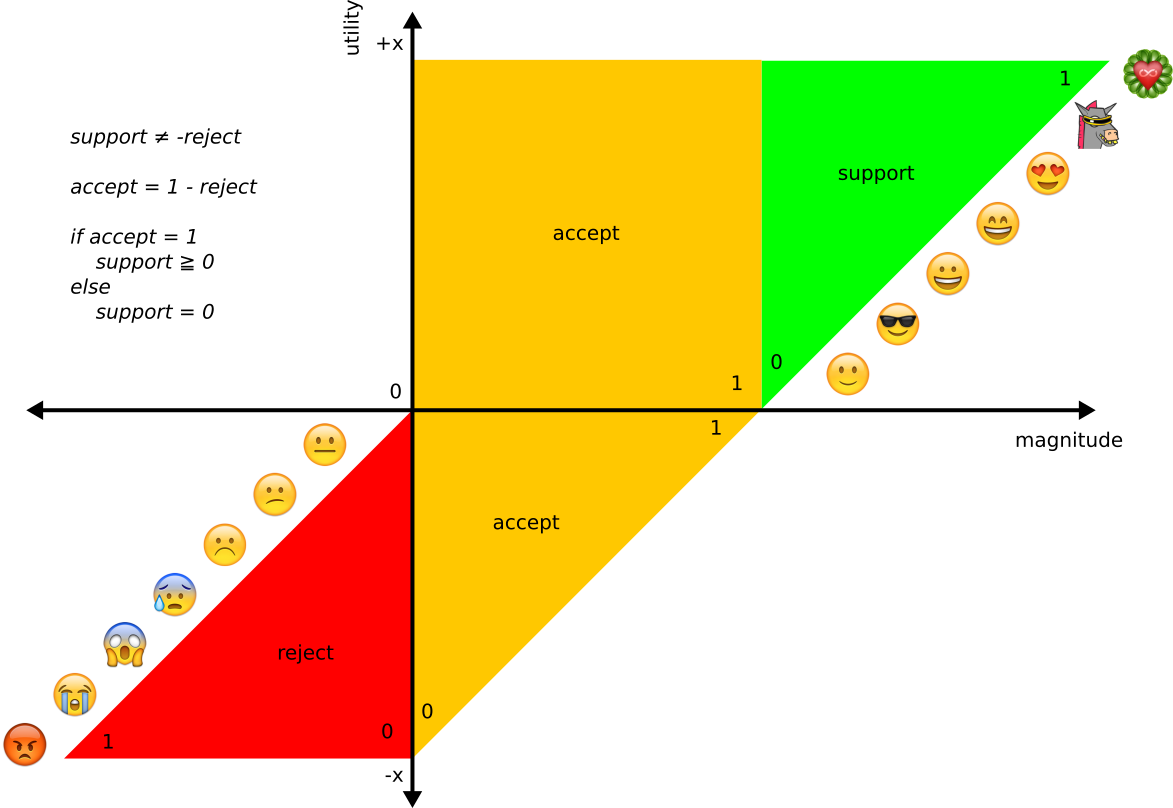
Games
The issue of potential domination in informal situation is addressed with two group approaches.
The consensus approach is a compromize approach in which the most accepted option of the whole is selected. The good thing is that the number of individuals unhappy with an outcome is minimized, reducing the potential for conflict and fragmentation. The bad thing is that a dominative minority can manipulate an honest majority into accepting their preference. strong inclusion criteria, Veto, Formal Consensus, Facilitation
Considering an unenforced association of cooperations: Most support → Domination of minorities → Frustration, fragmentation, loss of diversity, loss of cooperativeness. Most acceptance → Suppression of support majority → Frustration, increased exclusivity → limitation of growth increased dishonesty → loss of cooperativeness consideration of support → domination of superminorities
An example score voting game operating with this majoritarian meme is shown in Game A
- Players numerically score each option from a linear range.
- Scores for each option are tallied, multiplied by the corresponding score value then summed.
- The option with the highest sum is selected.
Game A is susceptible to selecting options with higher potential for minoritization and conflict over options with significantly lower potentials for the same, but fractionally lower total scores. Further, on a linear range it can be difficult to determine what is being expressed: whilst verbal indicators may provide some psychological anchoring ('score 10 for maximum support, 1 for maximum resistance, etc') manipulation by exaggeration to secure can obfuscate is a strateg it is difficult to determine exactly what is being expressed. Does 0 imply strongly disliked or simply the least liked? Does 6 imply strongly liked or simply most liked? And does 3 imply neither liked or disliked or simply the average feeling towards the available options?
WCS w. complete honesty
Minoritization or conflict. The option with the highest score could be chosen over another option with with a lower score
Consider to be an unenforced association of cooperative individuals, . Since the potential of a group increases as some function of , number of members, it behaves inclusively (at least not exclusively) in order to grow and better achieve its goals. Due to this inclusivity, there may exist a minority of dominative individuals among a supermajority who might try to manipulate a voting system if possible.
"An individual "manipulates" the voting scheme, if, by misrepresenting their preferences, they secure an outcome they prefer to the "honest" outcome - the choice the community would make if the individual expressed their true preferences."
Allan Gibbard, Manipulation of Voting Schemes: A General Result (1973). [De-gendered]
Assuming that above a critical ratio of , corrective action is taken perceived group outcome has a marked reinforcing effect on the members of a group cite, and manipulation by ///basically, pdom are only considered as a minority, they self-limit by destroying host.
where options which most group members do not resist are selected over options with more resistance - even if they have more support. This behaviour seeks to identify options with less conflict potential, greater harmony and increased likelihood of implementation.
- Unenforced groups are created and maintained by choice and activity within them is also made by choice.
- Once formed, groups are meta-stable. Fragmentation ultimately due to individuals getting better use from their time and energy elsewhere.
- due to conflict: dealing with conflict consumes resources, makes working hard, not fun
- dragging along a few:
- dragging down many: high energy path blocked, not fun
- function = energy * group size
- If people cannot express themselves fully, they won't. Individuals must be able to meaningfully express support, resistance and neither.
- A small amount of resistance can undermine efforts requiring widespread cooperation.
- A small amount of support can encourage widespread cooperation of accepting individuals.
- The discontent an individual suffers from an outcome they accept instead of support << than from an outcome they resist instead of support.
Game B
Acceptance is king.
- Score options (including 'status quo' and 'further options') using the resistance range {0, -1, -2, -3, -4, -5, -6}
- Tally scores.
- Select option with most acceptance.
- If there is a tie for most acceptance, re-score tied options using the support range {0, +1, +2, +3, +4, +5, +6}
- Tally scores.
- Select option with most support.
- If there is a tie for most support, flip a coin.
| Score | Acceptance = 1-Resistance |
|---|---|
| 0 | 100 % |
| -1 | 83 % |
| -2 | 67 % |
| -3 | 50 % |
| -4 | 33 % |
| -5 | 17 % |
| -6 | 0 % |
| Score | Support |
|---|---|
| +6 | 100 % |
| +5 | 83 % |
| +4 | 67 % |
| +3 | 50 % |
| +2 | 33 % |
| +1 | 17 % |
| 0. | 0 % |
Commentary
WCS w. complete honesty
Suppresion of support supermajority. The option with most acceptance could be selected over another option with fractionally less acceptance but overwhelmingly more support. The selected option has a lower likelihood of being implemented.
WCS w. some dishonesty
Dishonest suppresion of support supermajority. 'Down-shifting', a kind of exaggeration, is a dominant strategy whereby a player scores their least favoured option with -6, their most favoured option with 0. This strategy can be seen as pretending the initial range of {0, -1, -2, -3, -4, -5, -6} is actually {+3, +2, +1, 0, -1, -2, -3}. Further, a player can 'block' the support scores of all options except their favorite by scoring their non-favorite options between -6 and -1.
WCS w. complete dishonesty
Game B transforms into a dishonest analogue of game A. 'Down-shifting' quickly becomes the dominant strategy for all players as soon as some players start to use it. Then, as a game, A becomes identical to using any other cardinal, linear range such as {0, +1, +2, +3, +4, +5, +6} and selecting the highest rated option (See game A). - the use of a different range may have a psychological effect.
Game C
Acceptance is king, but you can express support without a tie.
- Score options (including 'status quo' and 'further options') using the range {+3, +2, +1, 0, -1, -2, -3}
- Tally scores.
- Select option with most acceptance.
1.If there is a tie for most acceptance, select option with most support.
- If there is a tie for most support, flip a coin.
| Score | Acceptance = 1-Resistance | Support |
|---|---|---|
| +3 | 1.00 | 1.00 |
| +2 | 1.00 | 0.67 |
| +1 | 1.00 | 0.33 |
| 0 | 1.00 | 0.00 |
| -1 | 0.67 | 0.00 |
| -2 | 0.33 | 0.00 |
| -3 | 0.00 | 0.00 |
Commentary
Game C is very similar to game B, except that the resistance and support ranges have been fused together; This permits better player expression since in game B ratings are likely to be less honest and, subsequently, the second round of scoring for support is likely to be a rare event. Since the selection rule remains the same, the WCSs and strategies are similar.
WCS w. complete honesty
Suppresion of support supermajority (visible). As before, the option with most acceptance could be selected over another option with fractionally less acceptance but overwhelmingly more support (e.g. A:100, S:0 > A:99, S:99). The selected option has a lower likelihood of being implemented. Now visible, there may be a discontent in the supermajority and guilt in the minority, who are now perhaps willing to accept the option knowing the opinions of the fellow players.
WCS w. some dishonesty
Dishonest suppresion of support supermajority (visible). As before, 'down-shifting', is a dominant strategy whereby a player scores their least favoured option with -3, their most favoured option with +3. Further, a player can 'block' the support scores of all options except their favorite by scoring their non-favorite options between -3 and -1.
WCS w. complete dishonesty
Game C transforms into a dishonest analogue of game A. As before, 'down-shifting' quickly becomes the dominant strategy for all players as soon as some players start to use it - although perhaps it is not as severe as in game B. Then, as a game, C becomes identical to using any other cardinal, linear range such as {0, +1, +2, +3, +4, +5, +6} and selecting the highest rated option (See game A). The use of a different range may have a psychological effect.
Game D
Acceptance is still king, but support is cautiously considered.
Preparation
Before scoring, the group must decide a value for , where
As ↑,
- likelihood of selecting options which suppress a support supermajority ↑
- minority manipulation potential ↑
- likelihood of selecting options leading to minoritization ↓
- likelihood of selecting options leading to conflict ↓
When selecting a value for the group should bear in mind that
- If → game D collapses to game A
- If → game D collapses to game C collapses to a dishonest analogue of game A
- If → game D remains distinct
- Score options (including 'status quo' and 'further options') using the range {+3, +2, +1, 0, -1, -2, -3}
- Tally scores.
- Select option with greatest .
- If there is a tie for greatest , select option with most support.
- If there is a tie for most support, flip a coin.
- If there is a tie for greatest , select option with most support.
| Score | Acceptance = 1-Resistance | Support |
|---|---|---|
| +3 | 1.00 | 1.00 |
| +2 | 1.00 | 0.67 |
| +1 | 1.00 | 0.33 |
| 0 | 1.00 | 0.00 |
| -1 | 0.67 | 0.00 |
| -2 | 0.33 | 0.00 |
| -3 | 0.00 | 0.00 |
Commentary
Now, if 𝛼 =10, A:100, S:0 < A:91, S:91. 𝛼 could be varied according to group priority of acceptance over activity. A:60, S:5 > A:50, S:50 > A:54, S:0 Game D is similar to game C, except that supports scores are now considered in the decision rule. Now, a minority of players are less able to dishonestly 'block' a support supermajority leading to dishonesty being disinsentivized. However, now a minority of players who honestly resist an option may be over-ruled. Varying the value of 𝛼 will
WCS w. complete honesty
Minoritization or conflict.
Semi-honest exaggeration. Best +3, worst -3 then accordingly distribute rest across range with accepted options in 0 to +3, supported options in +1 to +3 and resisted options in -3 to -1 (The semantics are finally good!)